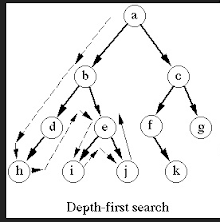
4 Applications for DFS and BFS
1- Count Numbers of Connected Component : __________________________________________________ #include <bits/stdc++.h> using namespace std ; #define endl '\n' #define ll long long const int N = 5e5 + 4 ; vector < int > adjlist [ N ]; bool visited [ N ]; int numo_f_Components = 0 ; int n , m ; void dfs ( int node){ if ( visited [node]== 1 ) return ; visited [node]= true ; for ( auto newnode : adjlist [node]) dfs( newnode ); } int main () { cin >> n >> m ; for ( int i = 0 ; i < m ; i ++){ int x , y ; cin >> x >> y ; adjlist [ x ].push_back( y ); adjlist [ y ].push_back( x ); } for ( int i = 0 ; i < n ; i ++){ if (! visited [ i ]) { numo_f_Components ++; dfs( i ); } } return 0 ; } _____________________________________________________________________________________________________ 2-the vertix belongs to which component (DFS) ____________...