Graph Theory(Breadth First Search)

Hellllo, guys new article again WOwwwww  in this article I will talk about another search way in 

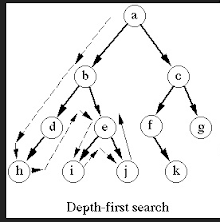
graph topic, which is DFS.
  

first, let's speak about how it's working??


ok, as you see now in this image Bfs is working by search level by level it searches in the level one 

first then when it's complete level one it starts a search in the next level and so on.

(notes that Bfs work in an unweighted graph  or weighted graph with equal-weighted)

(notes that Bfs is used to search to the shortest path)  EXAMPLE:(maze solver)

now, we wanna ask a question how can i know the level of the node in implementation?

we will write this algorithm by using a queue of pair the first one will be the value of the node and the second one will be the level .

Like:

  vector<int> BFS(int s, vector<vector<int> > & adjList) {
vector<int> len(sz(adjList), OO);  //oo is define to infinity
queue< pair<int, int> > q;
q.push(MP(s, 0)), len[s] = 0;

int cur, dep;
while(!q.empty()) {
pair<int, int> p = q.front(); q.pop();
cur = p.first, dep = p.second;

rep(i, adjList[cur]) if (len[adjList[cur][i]] == OO)
q.push(MP(adjList[cur][i], dep+1)), len[adjList[cur][i]] = dep+1;
}

return len; //cur is the furthest node from s with depth dep
}


ok we can implement this code by another way which is process the graph level by level

Like:
 
vector<int> BFS2(int s, vector<vector<int> > & adjList) {
vector<int> len(sz(adjList), OO);
queue<int> q;
q.push(s), len[s] = 0;

int dep = 0, cur = s, sz = 1;
for (; !q.empty(); ++dep, sz = q.size()) {
while (sz--) {
cur = q.front(), q.pop();
rep(i, adjList[cur]) if (len[adjList[cur][i]] == OO)
q.push(adjList[cur][i]), len[adjList[cur][i]] = dep+1;
}
}
return len; //cur is the furthest node from s with depth dep
}






























Comments

Post a Comment

Popular posts from this blog

Leet code (Reverse Integer)

  7.   Reverse Integer Given a signed 32-bit integer  x , return  x  with its digits reversed . If reversing  x  causes the value to go outside the signed 32-bit integer range  [-2 31 , 2 31  - 1] , then return  0 . Assume the environment does not allow you to store 64-bit integers (signed or unsigned).   Example 1: Input: x = 123 Output: 321 Example 2: Input: x = -123 Output: -321 Example 3: Input: x = 120 Output: 21 Example 4: Input: x = 0 Output: 0   Constraints: -2 31  <= x <= 2 31  - 1 Solution class Solution { public:     int reverse(int x) {         int rev = 0;         while (x) {             int pop = x % 10;             x /= 10;             if (rev > INT_MAX/10 || (rev == INT_MAX / 10 && pop > 7)) return 0;           ...
Read more

Graph Theory(adjacency matrix,adjacency list)

Image
today I will speak about one of the most important topics which are graph theory. I will take a long time in this series because I wanna speak a lot of data structure related to graph theory but in the beginning, I will speak about just two representations which are  (adjacency matrix, adjacency list). adjacency matrix the first let's talk about adjacency matrix .this to make a memory representation for any graph (directed or non-directed) we can imagine that Like  code bool adjacency_matrix[100][100];        Example n=3 0 1 0 1 1 0 0 1 1 for(int i=0;i<n;i++) for(int j=0;j<;j++){ int x; cin>>x; adjacency_matrix[i][j]=x; } adjacency list then I will speak about adjacency list, how to represent it in memory and how we implement it with code code vector< vector<int> > adjList1;               if adjacency list without  weight vector< vector< pair<int, int> ...
Read more

Recursion(Part 1)

In this article I will speak about one of the main topics in computer science and I will write some examples to make you know what is that and how you should use it.   Recursion function it’s a function call itself. And this function is consisting of three parts (Base Case, some Logic,  Sub-problem). 1-Base case: this is a case when it happens this recursion function should stop and gave you the result.     2- some Logic: which happens when function called himself. 3- Sub-problem: in this part, the function calls itself by part of it but this calling should never go to infinity. Ex1: void SayHello(int num) {     if(num < 1)                                                     ...
Read more